Calculating the Sum of a List of Numbers

We will begin our investigation with a simple problem that you already know how to solve without using recursion. Suppose that you want to calculate the sum of a list of numbers such as: $[1, 3, 5, 7, 9]$. An iterative function that computes the sum is shown below. The function uses an accumulator variable (total) to compute a running total of all the numbers in the list by starting with $0$ and adding each number in the list.

def iterative_sum(numbers):
    total = 0
    for n in numbers:
        total = total + n
    return total

iterative_sum([1, 3, 5, 7, 9])  # => 25

Pretend for a minute that you do not have while loops or for loops. How would you compute the sum of a list of numbers? If you were a mathematician you might start by recalling that addition is a function that is defined for two parameters, a pair of numbers. To redefine the problem from adding a list to adding pairs of numbers, we could rewrite the list as a fully parenthesized expression. Such an expression looks like this:

We can also parenthesize the expression the other way around,

Notice that the innermost set of parentheses, $(7 + 9)$, is a problem that we can solve without a loop or any special constructs. In fact, we can use the following sequence of simplifications to compute a final sum.

How can we take this idea and turn it into a Python program? First, let’s restate the sum problem in terms of Python lists. We might say the the sum of the list numbers is the sum of the first element of the list (numbers[0]), and the sum of the numbers in the rest of the list (numbers[1:]). To state it in a functional form:

In this equation $first(numbers)$ returns the first element of the list and $rest(numbers)$ returns a list of everything but the first element. This is easily expressed in Python as:

def sum_of(numbers):
    if len(numbers) == 0:
        return 0

    return numbers[0] + sum_of(numbers[1:])

sum_of([1, 3, 5, 7, 9])  # => 25

There are a few key ideas in this code sample to look at. First, on line 2 we are checking to see if the list is empty. This check is crucial and is our escape clause from the function. The sum of a list of length 0 is trivial; it is just zero. Second, on line 5 our function calls itself! This is the reason that we call the sum_of algorithm recursive. A recursive function is a function that calls itself.

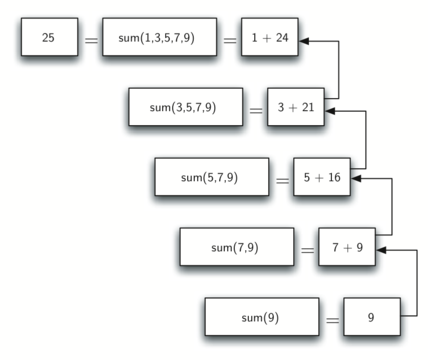
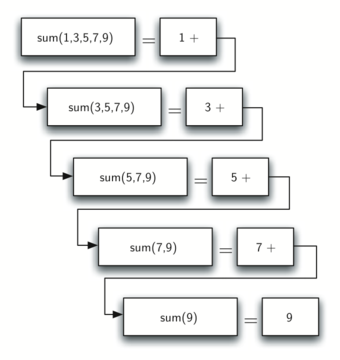
The diagram below shows the series of recursive calls that are needed to sum the list $[1, 3, 5, 7, 9]$. You should think of this series of calls as a series of simplifications. Each time we make a recursive call we are solving a smaller problem, until we reach the point where the problem cannot get any smaller.

When we reach the point where the problem is as simple as it can get, we begin to piece together the solutions of each of the small problems until the initial problem is solved. The diagram below shows the additions that are performed as sum_of works its way backward through the series of calls. When sum_of returns from the topmost problem, we have the solution to the whole problem.