The Sequential Search
When data items are stored in a collection such as a list, we say that they have a linear or sequential relationship. Each data item is stored in a position relative to the others. In Python lists, these relative positions are the index values of the individual items. Since these index values are ordered, it is possible for us to visit them in sequence. This process gives rise to our first searching technique, the sequential search.
The diagram below shows how this search works. Starting at the first item in the list, we simply move from item to item, following the underlying sequential ordering until we either find what we are looking for or run out of items. If we run out of items, we have discovered that the item we were searching for was not present.
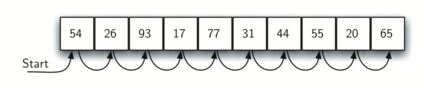
The Python implementation for this algorithm is shown below. The function needs the list and
the item we are looking for and returns a boolean value as to whether it
is present. Remember in practice we would use the Python in operator for this purpose, so you can think of the below algorithm as what we would do if in were not provided for us.
def sequential_search(alist, item):
position = 0
while position < len(alist):
if alist[position] == item:
return True
position = position + 1
return False
testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
sequential_search(testlist, 3) # => False
sequential_search(testlist, 13) # => True
Analysis of Sequential Search
To analyze searching algorithms, we need to decide on a basic unit of computation. Recall that this is typically the common step that must be repeated in order to solve the problem. For searching, it makes sense to count the number of comparisons performed. Each comparison may or may not discover the item we are looking for. In addition, we make another assumption here. The list of items is not ordered in any way. The items have been placed randomly into the list. In other words, the probability that the item we are looking for is in any particular position is exactly the same for each position of the list.
If the item is not in the list, the only way to know it is to compare it against every item present. If there are items, then the sequential search requires comparisons to discover that the item is not there. In the case where the item is in the list, the analysis is not so straightforward. There are actually three different scenarios that can occur. In the best case we will find the item in the first place we look, at the beginning of the list. We will need only one comparison. In the worst case, we will not discover the item until the very last comparison, the nth comparison.
What about the average case? On average, we will find the item about halfway into the list; that is, we will compare against items. Recall, however, that as n gets large, the coefficients, no matter what they are, become insignificant in our approximation, so the complexity of the sequential search, is :
| Case | Best Case | Worst Case | Average Case |
|---|---|---|---|
| item is present | |||
| item is not present |
We assumed earlier that the items in our collection had been randomly placed so that there is no relative order between the items. What would happen to the sequential search if the items were ordered in some way? Would we be able to gain any efficiency in our search technique?
Assume that the list of items was constructed so that the items were in ascending order, from low to high. If the item we are looking for is present in the list, the chance of it being in any one of the n positions is still the same as before. We will still have the same number of comparisons to find the item. However, if the item is not present there is a slight advantage. The diagram below shows this process as the algorithm looks for the item 50. Notice that items are still compared in sequence until 54. At this point, however, we know something extra. Not only is 54 not the item we are looking for, but no other elements beyond 54 can work either since the list is sorted.
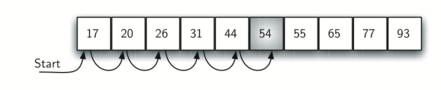
In this case, the algorithm does not have to continue looking through all of the items to report that the item was not found. It can stop immediately. The code below shows this variation of the sequential search function.
def ordered_sequential_search(alist, item):
position = 0
while position < len(alist):
if alist[position] == item:
return True
if alist[position] > item:
return False
position = position + 1
return False
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
ordered_sequential_search(testlist, 3) # => False
ordered_sequential_search(testlist, 13) # => True
The table below summarizes these results. Note that in the best case we might discover that the item is not in the list by looking at only one item. On average, we will know after looking through only items. However, this technique is still . In summary, a sequential search is improved by ordering the list only in the case where we do not find the item.
| Case | Best Case | Worst Case | Average Case |
|---|---|---|---|
| item is present | |||
| item is not present |