Binary Search Trees

So far we have seen two different ways to implement the map abstract data type—binary search on a list, and hash tables. In this section we will consider the binary tree, which is the basis of another common implementation of maps focused on efficient searching.

Before we look at the implementation, let’s review the interface provided by the map ADT. Notice that this interface is very similar to the Python dictionary.

• Map() Create a new, empty map.
• put(key, val) Add a new key-value pair to the map. If the key is already in the map then replace the old value with the new value.
• get(key) Given a key, return the value stored in the map or None otherwise.
• del Delete the key-value pair from the map using a statement of the form del map[key].
• len() Return the number of key-value pairs stored in the map.
• in Return True for a statement of the form key in map, if the given key is in the map.

Implementation

A binary search tree relies on the property that keys that are less than the parent are found in the left subtree, and keys that are greater than the parent are found in the right subtree. We will call this the BST property. As we implement the Map interface as described above, the BST property will guide our implementation. The diagram below illustrates this property of a binary search tree, showing the keys without any associated values. Notice that the property holds for each parent and child. All of the keys in the left subtree are less than the key in the root; all of the keys in the right subtree are greater than the root.

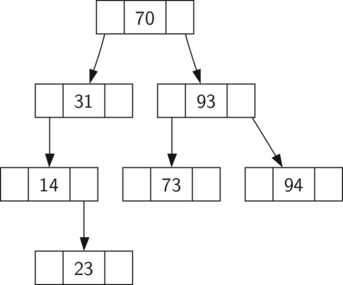
Now that you know what a binary search tree is, we will look at how a binary search tree is constructed. The search tree above represents the nodes that exist after we have inserted the following keys in the order: $70, 31, 93, 94, 14, 23, 73$. Since 70 was the first key inserted into the tree, it is the root. Next, 31 is less than 70, so it becomes the left child of 70. Next, 93 is greater than 70, so it becomes the right child of 70. Now we have two levels of the tree filled, so the next key is going to be the left or right child of either 31 or 93. Since 94 is greater than 70 and 93, it becomes the right child of 93. Similarly 14 is less than 70 and 31, so it becomes the left child of 31. 23 is also less than 31, so it must be in the left subtree of 31. However, it is greater than 14, so it becomes the right child of 14.

To implement the binary search tree, we will use the nodes and references approach. While it would be possible in Python to implement the tree using dicts as we have elsewhere in this chapter, doing so presupposes that we have the very associative structure that we are implementing!

Our implementation will use two classes: TreeNode to house the lower level logic to construct and manipulate the tree itself, and BinarySearchTree to hold a reference to the root node and provide a map-like interface to the user.

The TreeNode class provides many helper functions that make the work done in the BinarySearchTree class methods much easier. The constructor for a TreeNode, along with these helper functions, is shown below. As you can see, many of these helper functions help to classify a node according to its own position as a child, (left or right) and the kind of children the node has. The TreeNode class will also explicitly keep track of the parent as an attribute of each node. You will see why this is important when we discuss the implementation for the del operator.

One of the more interesting methods of TreeNode provides an interface to simply iterate over all the keys in the tree in order. You already know how to traverse a binary tree in order, using the inorder traversal algorithm. However, because we want our iterator to operate lazily, in this case we use the yield keyword to define our __iter__ method as a Python generator. Pay close attention to the __iter__ implementation as at first glance you might think that the code is not recursive: in fact, because __iter__ overrides the for x in operation for iteration, it really is recursive!

Our full implementation of TreeNode is provided below. It includes three further methods find_successor, find_min and splice_out which you can ignore for now as we will return to them later when discussing deletion.

class TreeNode(object):

    def __init__(self, key, val, left=None, right=None, parent=None):
        self.key = key
        self.val = val
        self.left = left
        self.right = right
        self.parent = parent

    def is_left_child(self):
        return self.parent and self.parent.left == self

    def is_right_child(self):
        return self.parent and self.parent.right == self

    def is_leaf(self):
        return not (self.right or self.left)

    def has_any_children(self):
        return self.right or self.left

    def has_both_children(self):
        return self.right and self.left

    def has_one_child(self):
        return self.has_any_children() and not self.has_both_children()

    def replace_node_data(self, key, val, left, right):
        self.key = key
        self.val = val
        self.left = left
        self.right = right
        if self.left:
            self.left.parent = self
        if self.right:
            self.right.parent = self

    def __iter__(self):
        if self is None:
            return

        if self.left:
            # `in` calls `__iter__` so is recursive
            for elem in self.left:
                yield elem

        yield self.key

        if self.right:
            # recurse again
            for elem in self.right:
                yield elem

    def find_successor(self):
        if self.right:
            return self.right.find_min()

        if self.parent is None:
            return None

        if self.is_left_child():
            return self.parent

        self.parent.right = None
        successor = self.parent.find_successor()
        self.parent.right = self
        return successor

    def find_min(self):
        current = self
        while current.left:
            current = current.left
        return current

    def splice_out(self):
        if self.is_leaf():
            if self.is_left_child():
                self.parent.left = None
            else:
                self.parent.right = None

        else:
            promoted_node = self.left or self.right

            if self.is_left_child():
                self.parent.left = promoted_node
            else:
                self.parent.right = promoted_node
            promoted_node.parent = self.parent

    

Now that we have our TreeNode class we can begin to write BinarySearchTree itself. Recall that the core functionality of this class will be to enable puting to and geting from the tree, so we begin our implementation with the put functionality.

In order to enable the tree[1] = 'foo' style assignment interface for our BinarySearchTree instances, we override the __setitem__ magic method. In this method we first check to see if the tree already has a root. If there is not a root then we create a new TreeNode and set it as the root of the tree. If a root node is already in place then put calls the private, recursive, helper function _put to search the tree according to the following algorithm:

• Starting at the root of the tree, search the binary tree comparing the new key to the key in the current node. If the new key is less than the current node, search the left subtree. If the new key is greater than the current node, search the right subtree.
• When there is no left (or right) child to search, we have found the position in the tree where the new node should be installed.
• To add a node to the tree, create a new TreeNode object and insert the object at the point discovered in the previous step.

The code below shows the Python code for inserting a new node in the tree. The _put function is written recursively following the steps outlined above. Notice that when a new child is inserted into the tree, the node is passed to the new tree as the parent.

One important problem with our implementation of insert is that duplicate keys are not handled properly. As our tree is implemented a duplicate key will create a new node with the same key value in the right subtree of the node having the original key. The result of this is that the node with the new key will never be found during a search. A better way to handle the insertion of a duplicate key is for the value associated with the new key to replace the old value. We leave fixing this bug as an exercise for you.

class BinarySearchTree(object):

    TreeNodeClass = TreeNode

    def __init__(self):
        self.root = None
        self.size = 0

    def __len__(self):
        return self.size

    def __iter__(self):
        return self.root.__iter__()

    def __setitem__(self, key, val):
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = self.TreeNodeClass(key, val)
        self.size = self.size + 1

    def _put(self, key, val, node):
        if key < node.key:
            if node.left:
                self._put(key, val, node.left)
            else:
                node.left = self.TreeNodeClass(key, val, parent=node)
        else:
            if node.right:
                self._put(key, val, node.right)
            else:
                node.right = self.TreeNodeClass(key, val, parent=node)

    

The diagram below illustrates the process for inserting a new node into a binary search tree. The lightly shaded nodes indicate the nodes that were visited during the insertion process.

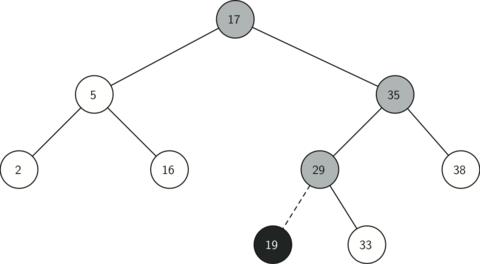
Once the tree is constructed, the next task is to implement the retrieval of a value for a given key. The get functionality is even easier than the put functionality because we simply search the tree recursively until we get to a non-matching leaf node or find a matching key. When a matching key is found, the value stored in the val of the node is returned.

Again, inorder to enable a tree[1] retrieval interface, we overload one of Python’s magic methods—in this case __getitem__. Just like with __setitem__, the primary purpose of this method is to handle presence and absence of a root node, and delegates the core get functionality to _get.

The search code in the _get method uses the same logic for choosing the left or right child as the _put method. Notice that the _get method returns a TreeNode to __getitem__, this allows _get to be used as a flexible helper method for other BinarySearchTree methods that may need to make use of other data from the TreeNode besides the val.

    def __getitem__(self, key):
        if self.root:
            result = self._get(key, self.root)
            if result:
                return result.val
        raise KeyError

    def _get(self, key, node):
        if not node:
            return None
        if node.key == key:
            return node
        if key < node.key:
            return self._get(key, node.left)
        return self._get(key, node.right)

    

Using _get, we can implement the in operation by writing a __contains__ method for the BinarySearchTree. The __contains__ method will simply call _get and return True if _get returns a value, or False if it returns None. The code for __contains__ is shown below.

    def __contains__(self, key):
        return bool(self._get(key, self.root))
    

Finally, we turn our attention to the most challenging method in the binary search tree: the deletion of a key. The first task is to find the node to delete by searching the tree. If the tree has more than one node we search using the _get method to find the TreeNode that needs to be removed. If the tree only has a single node, that means we are removing the root of the tree, but we still must check to make sure the key of the root matches the key that is to be deleted. In either case if the key is not found the del operator raises an error.

    def delete(self, key):
        if self.size > 1:
            node_to_remove = self._get(key, self.root)
            if node_to_remove:
                self.remove(node_to_remove)
                self.size = self.size - 1
                return
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
            return

        raise KeyError('Error, key not in tree')

    def __delitem__(self, key):
        self.delete(key)
        

Once we’ve found the node containing the key we want to delete, there are three cases that we must consider:

1. The node to be deleted has no children
2. The node to be deleted has only one child
3. The node to be deleted has two children

The first case is straightforward. If the current node has no children all we need to do is delete the node and remove the reference to this node in the parent. The code for this case is shown below.

    def remove(self, node):
        if node.is_leaf() and node.parent is not None:
            if node == node.parent.left:
                node.parent.left = None
            else:
                node.parent.right = None
            

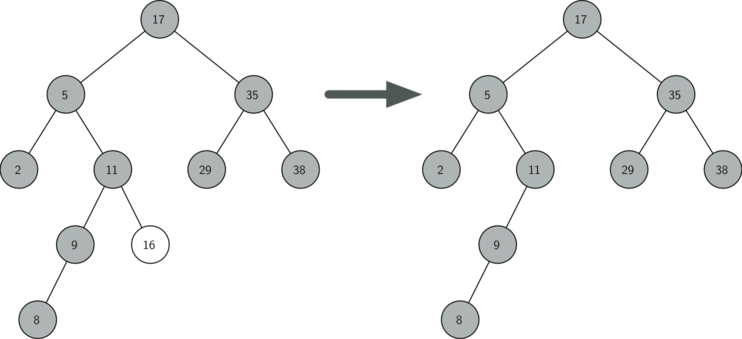
The second case is only slightly more complicated (see below). If a node has only a single child, then we can simply promote the child to take the place of its parent. The code for this case is shown in the next code sample. As you look at this code you will see that there are six cases to consider. Since the cases are symmetric with respect to either having a left or right child we will just discuss the case where the current node has a left child. The decision proceeds as follows:

1. If the current node is a left child then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the left child reference of the parent to point to the current node’s left child.
2. If the current node is a right child then we only need to update the parent reference of the right child to point to the parent of the current node, and then update the right child reference of the parent to point to the current node’s right child.
3. If the current node has no parent, it must be the root. In this case we will just replace the key, val, left, and right data by calling the replace_node_data method on the root.

Code for this decision process may look like:

        elif node.has_one_child():
            promoted_node = node.left or node.right

            if node.is_left_child():
                promoted_node.parent = node.parent
                node.parent.left = promoted_node
            elif node.is_right_child():
                promoted_node.parent = node.parent
                node.parent.right = promoted_node
            else:
                node.replace_node_data(
                    promoted_node.key,
                    promoted_node.val,
                    promoted_node.left,
                    promoted_node.right
                )

            

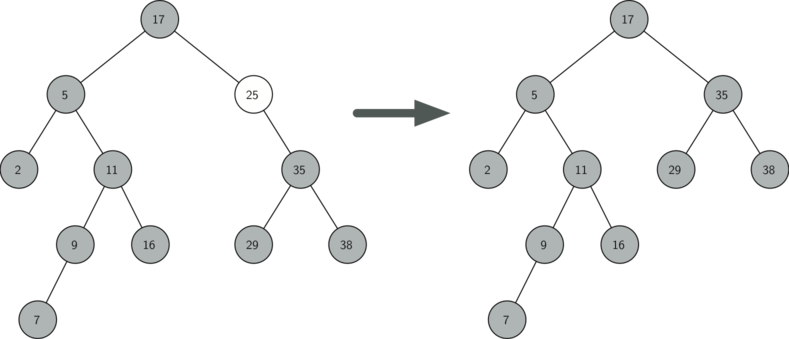
The third case is the most difficult case to handle (see below). If a node has two children, then it is unlikely that we can simply promote one of them to take the node’s place. We can, however, search the tree for a node that can be used to replace the one scheduled for deletion. What we need is a node that will preserve the binary search tree relationships for both of the existing left and right subtrees. The node that will do this is the node that has the next-largest key in the tree. We call this node the successor, and we will look at a way to find the successor shortly. The successor is guaranteed to have no more than one child, so we know how to remove it using the two cases for deletion that we have already implemented. Once the successor has been removed, we simply put it in the tree in place of the node to be deleted.

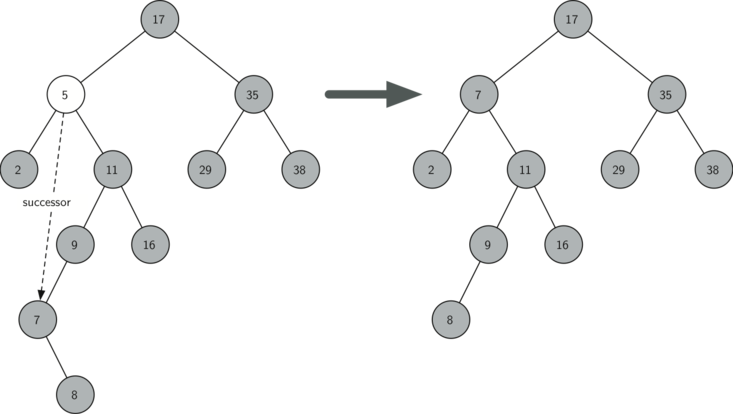
The code to handle the third case is shown below. Notice that we make use of the helper methods find_successor and find_min to find the successor. To remove the successor, we make use of the method splice_out. The reason we use splice_out is that it goes directly to the node we want to splice out and makes the right changes. We could call delete recursively, but then we would waste time re-searching for the key node.

        else:  # has both children
            successor = node.find_successor()
            if successor:
                successor.splice_out()
                node.key = successor.key
                node.val = successor.val
    

The code to find the successor is shown above and as you can see is a method of the TreeNode class. This code makes use of the same properties of binary search trees that cause an inorder traversal to print out the nodes in the tree from smallest to largest. There are three cases to consider when looking for the successor:

1. If the node has a right child, then the successor is the smallest key in the right subtree.
2. If the node has no right child and is the left child of its parent, then the parent is the successor.
3. If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.

The first condition is the only one that matters for us when deleting a node from a binary search tree.

The find_min method is called to find the minimum key in a subtree. You should convince yourself that the minimum valued key in any binary search tree is the leftmost child of the tree. Therefore the find_min method simply follows the left references in each node of the subtree until it reaches a node that does not have a left child.

Analysis

With the implementation of a binary search tree now complete, we will do a quick analysis of the methods we have implemented. Let’s first look at the put method. The limiting factor on its performance is the height of the binary tree. Recall that the height of a tree is the number of edges between the root and the deepest leaf node. The height is the limiting factor because when we are searching for the appropriate place to insert a node into the tree, we will need to do at most one comparison at each level of the tree.

What is the height of a binary tree likely to be? The answer to this question depends on how the keys are added to the tree. If the keys are added in a random order, the height of the tree is going to be around $\log_2{n}$ where $n$ is the number of nodes in the tree. This is because if the keys are randomly distributed, around half of them will be less than the root and half will be greater than the root. Remember that in a binary tree there is one node at the root, two nodes in the next level, and four at the next. The number of nodes at any particular level is $2^d$ where $d$ is the depth of the level. The total number of nodes in a perfectly balanced binary tree is $2^{h+1}-1$, where $h$ represents the height of the tree.

A perfectly balanced tree has the same number of nodes in the left subtree as it does in the right subtree. In a balanced binary tree, the worst-case performance of put is $O(\log_2{n})$, where $n$ is the number of nodes in the tree. Notice that this is the inverse relationship to the calculation in the previous paragraph. So $\log_2{n}$ gives us the height of the tree, and represents the maximum number of comparisons that put will need to do as it searches for the proper place to insert a new node.

Unfortunately it is possible to construct a search tree that has height $n$ simply by inserting the keys in sorted order! An example of such a tree is shown below. In this case the performance of the put method is $O(n)$.

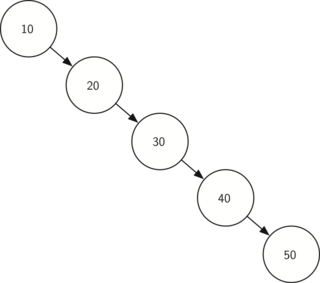
Now that you understand that the performance of the put method is limited by the height of the tree, you can probably guess that other methods, get, in, and del, are limited as well. Since get searches the tree to find the key, in the worst case the tree is searched all the way to the bottom and no key is found. At first glance del might seem more complicated, since it may need to search for the successor before the deletion operation can complete. But remember that the worst-case scenario to find the successor is also just the height of the tree which means that you would simply double the work. Since doubling is a constant factor it does not change worst case