Representing a Graph

In this section we will look at two common abstract representations of graphs: the adjacency matrix and the unfortunately named adjacency “list”. The adjacency list is really a mapping, so in this section we also consider two possible representations in Python of the adjacency list: one an object-oriented approach with a Python dict as its underlying data type, and one just using a plain dict directly.

It’s useful to be familiar with many ways to represent graphs as you will encounter them everywhere. Ultimately though, we see the adjacency list representation using a pure map type (such as a dict in Python) as the most intuitive and flexible.

The Adjacency Matrix

One of the easiest ways to implement a graph is to use a two-dimensional matrix. In this matrix implementation, each of the rows and columns represent a vertex in the graph. The value that is stored in the cell at the intersection of row $v$ and column $w$ indicates if there is an edge from vertex $v$ to vertex $w$. When two vertices are connected by an edge, we say that they are adjacent. The diagram below illustrates the adjacency matrix for the example graph we presented earlier. A value in a cell represents the weight of the edge from vertex $v$ to vertex $w$.

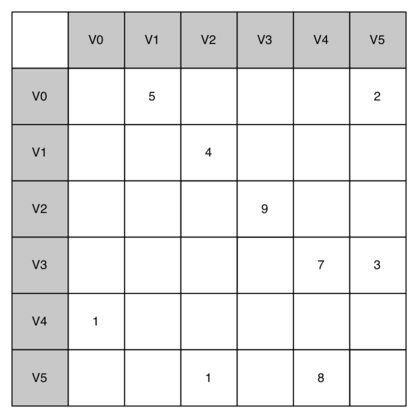
The advantage of the adjacency matrix is that it is simple, and for small graphs it is easy to see which nodes are connected to other nodes. However, notice that most of the cells in the matrix are empty. Because most of the cells are empty we say that this matrix is “sparse.” A matrix is not a very efficient way to store sparse data. In fact, in Python you must go out of your way to even create a matrix structure like the one above.

The adjacency matrix is a good implementation for a graph when the number of edges is large. But what do we mean by large? How many edges would be needed to fill the matrix? Since there is one row and one column for every vertex in the graph, the number of edges required to fill the matrix is $|V|^2$. A matrix is full when every vertex is connected to every other vertex. There are few real problems that approach this sort of connectivity. The problems we will look at in this section all involve graphs that are sparsely connected.

The Adjacency List

A more space-efficient way to implement a sparsely connected graph is to use the unfortunately named adjacency list structure. In an adjacency list implementation we keep a master collection of all the vertices in the Graph object and then each vertex object in the graph maintains a list of the other vertices that it is connected to. In our implementation of the Vertex class we will use a dictionary rather than a list as our master collection, where the dictionary keys are the vertices, and the values are the weights. The diagram below shows an adjacency list representation of the example graph we have been discussing.

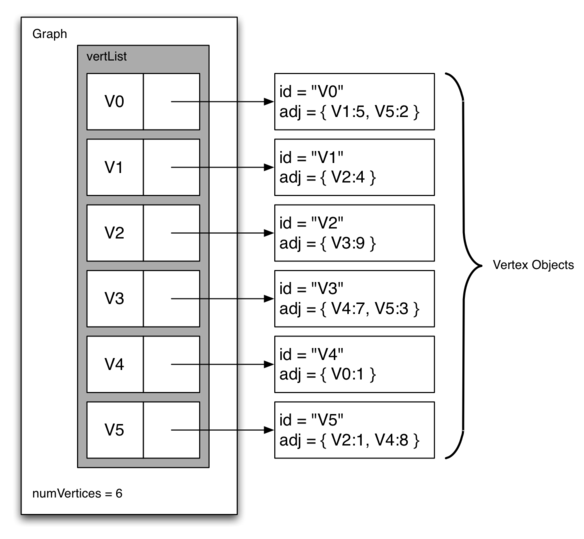
The advantage of the adjacency list implementation is that it allows us to compactly represent a sparse graph. The adjacency list also allows us to easily find all the links that are directly connected to a particular vertex.

An Object-Oriented Approach

Using dictionaries, it is easy to implement the adjacency list in Python. In this implementation we create two classes: Graph, which holds the master list of vertices, and Vertex, which will represent each vertex in the graph.

Each Vertex uses a dictionary to keep track of the vertices to which it is connected, and the weight of each edge. If we weren’t concerned with edge weights, we could use a set in place of a dictionary. This dictionary is called neighbors.

In the code below, the add_neighbor method is used to add a connection from this vertex to another. The get_connections method returns all of the vertices in the adjacency list, as represented by the neighbors instance variable. The get_weight method returns the weight of the edge from this vertex to the vertex passed as a parameter.

class Vertex(object):
    def __init__(self, key):
        self.key = key
        self.neighbors = {}

    def add_neighbor(self, neighbor, weight=0):
        self.neighbors[neighbor] = weight

    def __str__(self):
        return '{} neighbors: {}'.format(
            self.key,
            [x.key for x in self.neighbors]
        )

    def get_connections(self):
        return self.neighbors.keys()

    def get_weight(self, neighbor):
        return self.neighbors[neighbor]

The Graph class, shown below, contains a dictionary that maps vertex names to vertex objects. Graph also provides methods for adding vertices to a graph and connecting one vertex to another. The get_vertices method returns the names of all of the vertices in the graph. In addition, we have implemented the __iter__ method to make it easy to iterate over all the vertex objects in a particular graph. Together, the two methods allow you to iterate over the vertices in a graph by name, or by the objects themselves.

class Graph(object):
    def __init__(self):
        self.verticies = {}

    def add_vertex(self, vertex):
        self.verticies[vertex.key] = vertex

    def get_vertex(self, key):
        try:
            return self.verticies[key]
        except KeyError:
            return None

    def __contains__(self, key):
        return key in self.verticies

    def add_edge(self, from_key, to_key, weight=0):
        if from_key not in self.verticies:
            self.add_vertex(Vertex(from_key))
        if to_key not in self.verticies:
            self.add_vertex(Vertex(to_key))
        self.verticies[from_key].add_neighbor(self.verticies[to_key], weight)

    def get_vertices(self):
        return self.verticies.keys()

    def __iter__(self):
        return iter(self.verticies.values())

Using the Graph and Vertex classes just defined, the following Python session creates our example graph. First we create six vertices numbered 0 through 5. Then we display the vertex dictionary. Notice that for each key 0 through 5 we have created an instance of a Vertex. Next, we add the edges that connect the vertices together. Finally, a nested loop verifies that each edge in the graph is properly stored.

>>> g = Graph()
>>> for i in range(6):
...     g.add_vertex(Vertex(i))
>>> g.verticies
{0: <adjGraph.Vertex instance at 0x41e18>,
 1: <adjGraph.Vertex instance at 0x7f2b0>,
 2: <adjGraph.Vertex instance at 0x7f288>,
 3: <adjGraph.Vertex instance at 0x7f350>,
 4: <adjGraph.Vertex instance at 0x7f328>,
 5: <adjGraph.Vertex instance at 0x7f300>}
>>> g.add_edge(0, 1, 5)
>>> g.add_edge(0, 5, 2)
>>> g.add_edge(1, 2, 4)
>>> g.add_edge(2, 3, 9)
>>> g.add_edge(3, 4, 7)
>>> g.add_edge(3, 5, 3)
>>> g.add_edge(4, 0, 1)
>>> g.add_edge(5, 4, 8)
>>> g.add_edge(5, 2, 1)
>>> for v in g:
...     for w in v.get_connections():
...         print('{} -> {}'.format(v.key, w.key))
...
0 -> 5
0 -> 1
1 -> 2
2 -> 3
3 -> 4
3 -> 5
4 -> 0
5 -> 4
5 -> 2

Using Dictionaries Directly

As with our node and edges representation of trees, you may wonder whether it is worthwhile to wrap the underlying structure of our graph with classes as we have above. This will depend on the context, but our general preference is actually to work directly with the data structure. Doing so allows us to more easily print or otherwise debug a graph, create a graph as a literal composite type, and serialize a graph for instance to JSON.

The example graph above would simply look like:

{
    0: {1: 5, 5: 2},
    1: {2: 4},
    2: {3: 9},
    3: {4: 7, 5: 3},
    4: {0: 1},
    5: {4: 8}
}

For the remainder of the chapter, we will use dictionaries directly in most cases.